Les vies de Vishy

Cette énigme m’est venue suite aux longues et passionnantes conversations que j’ai pu avoir avec M. Léo Gerville-Réache que je remercie en cette occasion.
La situation décrite montre qu'un changement infime dans un énoncé peut entraîner un résultat totalement différent.
Vishy est un indien qui partage deux conceptions de la vie, malheureusement incompatibles :
- La première consiste à dire qu’il ne peut vivre qu’une seule fois.
- La seconde qu’il aura eu deux vies. Si tel était le cas, il serait incapable de dire si celle en cours est la première ou la seconde.
Vishy accorde à chaque théorie un degré de confiance de 50%. On supposera que cela équivaut à une probabilité de 50%. Il en déduit que la première théorie avec une seule vie est plausible à 50%, par définition. La seconde théorie propose deux vies dont on suppose l’équiprobabilité. Il obtient donc un ensemble de probabilités pour ces trois vies que l’on note (0,50 ; 0,25 ; 0,25). Rien de bien compliqué... si l'on admet la métempsychose.
Mais Vishy lit le paradoxe de la Belle au Bois Dormant. Et il se dit que si à chaque vie il se posait la question (ou si quelqu’un fortuitement l’interroge ou l’initie) sur savoir s’il évolue suivant les théories 1 ou 2, sa situation ressemblerait à celle de la Belle ! S’il suit ce qui est a été dit sur cette énigme (sur ce site ou chez d’autres auteurs), il devrait changer de probabilités et passer à (0,33 ; 0,33 ; 0,33) !
Le parallèle entre Vishy et la Belle est évident, même si Vishy définit lui-même les hypothèses, alors que la Belle est renseignée par un expérimentateur objectif.
Question
Comment pouvez-vous aider Vishy à surmonter cette apparente contradiction ?
Solution proposée
On peut effectivement être troublé par les ressemblances entre les deux énigmes :
- Vishy - Aurore,
- Vie 1 – lundi,
- Vie 2 – mardi,
- Question métaphysique - question de l’expérimentateur.
Pourquoi aboutit-on à deux ensembles de probabilités distincts ?
Dans un premier temps, on peut essayer de voir ce qui diffère dans les deux procédures.
- Les probabilités de Vishy sont données par lui-même ; ceux d’Aurore par l’observation des expérimentateurs.
- Allons plus loin, c’est Vishy ou un ami qui déclencherait la question métaphysique : on note qu’elle apparaîtrait quel que soit le scénario engagé. Vishy n’a aucune information par ce biais ! Pour Aurore, c’est le tirage au sort qui lance la procédure de l’entretien et ceci renseigne (si légèrement soit-il) Aurore sur le cours du processus.
Aurore a bien une information par la question de l’expérimentateur, mais pas Vishy. Les procédures sont donc différentes et ne permettent pas Vishy de modifier les probabilités de quelque manière que ce soit.
Dans un second temps, on peut essayer d’aller plus loin dans la description des deux procédures : faisons appel aux « chaînes de Markov » (Un article didactique est disponible sur le site Image des Maths du CNRS : "Markov et la Belle au bois dormant" Article ici ).
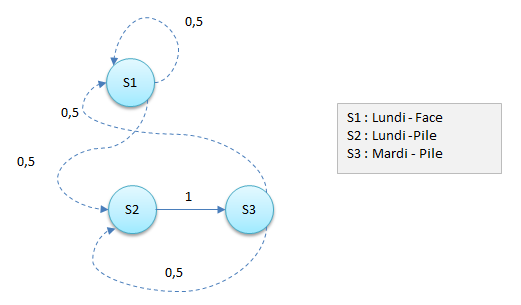
Pour Aurore on obtient :
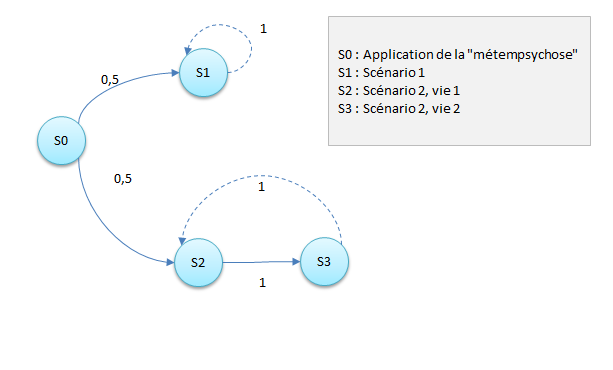
Pour Vishy on obtient un graphe où le "tirage au sort" n'a lieu qu'une seule fois. Il suppose que si on répète l'expérience avec d'autres mortels, on aurait toujours le même résultat :
Les deux graphes sont bien différents. Celui d’Aurore est classique. Sa matrice T de transitions est : $$\begin{align} T &=& \begin{pmatrix} 0,5 & 0 & 0,5 \\ 0,5 & 0 & 0,5 \\ 0 & 1 & 0 \end{pmatrix} \end{align}$$
Et son vecteur propre est : $$\begin{align} \vec{V_p} &=& \begin{pmatrix} 1/3 \\ 1/3 \\ 1/3 \end{pmatrix} \end{align}$$
Si on fait la somme des deux cas Face on retrouve bien au final (1/3 ; 2/3).
Pour Vishy, la matrice de transition est différente: $$\begin{align} T &=& \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0,5 & 1 & 0 & 0 \\ 0,5 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} \end{align}$$Son vecteur propre est particulier. (En fait il y a deux vecteurs propres distincts. Ainsi, la situation de départ compte.) Si l'on part du vecteur le plus à gauche sur le graphe \begin{align} \vec{V_{départ}} &=& \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \end{align} on obtient : $$\begin{align} \vec{V_p} &=& \begin{pmatrix} 0 \\ 1/2 \\ 1/4 \\ 1/4 \end{pmatrix} \end{align}$$
Vishy peut donc rester avec ses hypothèses (0,50 ; 0,25 ; 0,25) et n’a pas ici matière à se remettre en question.
Ceci montre qu'il faut une précision d'horloger : un simple changement et les aiguilles tournent dans le mauvais sens.
Si Markov dans une seconde vie croisait celle de Vishy, il lui dirait que sa théorie par les graphes ni ne conforte ni ne contredit les convictions de chacun !
