Take Five and More
M. Laurent Delabre, que je remercie, nous soumet cette énigme qui prolonge adroitement l'analyse de « Take Five » cliquez ici.:
Alice et Pascal lancent la lecture aléatoire d'un CD : une piste va être lue au hasard, il s'agit ou bien de Take Five 5 minutes, ou bien de Take Five 10 minutes (on suppose l'équiprobabilité). Alice n'a pas de montre et est seule à entendre et à être bercée par la musique dans son casque ; sans casque, son ami Pascal n'entend rien et peut consulter sa montre, observer Alice, l'interrompre pour lui poser une question. Take Five 10 minutes est très semblable à la version courte, si bien qu'on ne peut pas les différencier. Cette version longue est cependant extraordinaire, Alice et Pascal connaissent tous les deux son secret : des notes à effet hypnotique sont jouées durant la cinquième minute, et durant la sixième minute la personne qui les a entendues oublie tout ce qui lui est arrivé pendant les cinq dernières minutes écoulées, si bien qu'il lui semble qu'elle écoute la première minute du morceau ! Pour la personne hypnotisée, la musique est continue et semble ne durer que cinq minutes, rien ne peut lui permettre de distinguer un avant et un après hypnose. Alice sait aussi que Pascal va l'interrompre dans tous les cas lors de la deuxième minute, et en cas de version longue également lors de la septième minute de l'écoute, pour lui demander la probabilité qu'elle écoute la version courte.
Ce genre d’énigme a le mérite de vérifier si l’on maîtrise bien les précédents acquis et si l’on peut aller encore plus loin dans la difficulté. Aussi, après avoir proposé une démonstration « classique » parmi bien d’autres possibles, on proposera une résolution avec une chaîne de Markov. Cette façon de faire est un peu plus complexe, mais permet de représenter sous forme graphique et donc plus lisible le problème.
Voyez-vous une démonstration à ce type d’énigme ?
__________________________________________________________________________
1 - Démonstration directe
a) Rappelons la démonstration de la première version du problème :
- Si Fabienne arrive par le premier bus, elle autant de chance d’entendre la version courte que longue. On en déduit : $$P(courte, bus 1) = P(longue, bus 2)$$
- Si on a la version longue, Fabienne a autant de chance d’arriver par le premier ou le second bus : $$P(longue, bus 1) = P(longue, bus 2)$$
Donc, ces trois probabilités sont égales. On a la probabilité que Fabienne entende « Take Five » définie par : $$ \frac{P(longue, bus 1) + P(longue, bus 2) }{ P(courte, bus 1) + P(longue, bus 1) ) + P(longue, bus 2)} = \frac{2}{3} $$
b) Pour le second et nouveau problème, on a avantageusement remplacé le bus par un lecteur CD. Si l'on veut malgré tout rester avec nos bus, on ajoute le cas où après être arrivée par le premier bus et avoir écouté le début de la version longue, Fabienne écoute la seconde partie de cet air de jazz. Si on suppose que d’un côté elle a parfaitement oublié 5 minutes de son existence, que l'on ne se repose la question qu’une seule fois et une seule et que tous nous sommes parfaitement au courant de ce phénomène hypnotique, on peut alors admettre qu’elle écoutera autant de fois la première partie du morceau que la seconde : $$P(longue, bus 1) = P’(longue, bus 1)$$
On obtient 4 probabilités qui sont égales (au lieu de 3 pour le problème original), dont trois pour la version longue. La probabilité d'écouter la version longue devient : $$ \frac{P(longue, bus 1) + P’(longue, bus 1) + P(longue, bus 2) }{P(courte, bus 1) + P(longue, bus 1) + P’(longue, bus 1) + P(longue, bus 2)} = \frac{3}{4} $$
Cette hypnose fait passer la probabilité de 2/3 à 3/4 pour la version longue.2 - Démonstration par une Chaîne de Markov
On remarque que d’écouter la version longue deuxième partie est possible de deux façons différentes dont les probabilités sont P(longue, bus 2) et P’(longue, bus 1). Que se passerait-il si on imaginait un opéra complet de plusieurs heures et des bus arrivant toutes les trois minutes ? On aurait vite des problèmes d’écriture !
Face à des problèmes aussi lourds Il existe une manière de s’y retrouver : les chaînes de Markov (dont je prépare un article à ce sujet). Elles sont abordées au niveau licence, mais la plupart du temps ne demande pas une connaissance mathématique complète. Ici, elle sert surtout à illustrer de façon graphique la différence entre les deux problèmes.
Pour le problème original, il y a plusieurs manières de faire. Ici j’ai choisi de définir quatre états S0, S1, S2 et S3. S0 définit le point de départ de l’expérience : Fabienne attend son bus. Les trois états suivants sont ceux retenus à la fin de l’expérience. Fabienne a autant de chance de passer de S0 à l’un de ces trois états. Les probabilités de transitions sont 1/3.
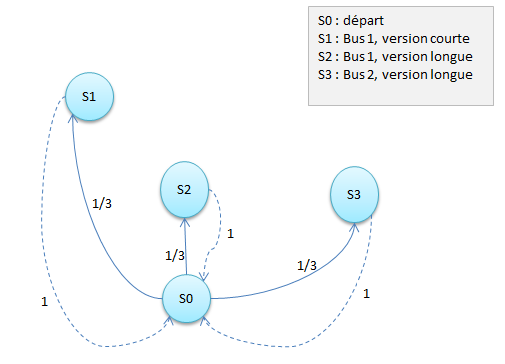
Si l’on renouvelle l’expérience disons les jours suivants, on passe d’un état S1, S2 ou S3 à celui de départ S0 (de façon certaine, donc on a des probabilités de transitions égales à 1).
La matrice de transition est : $$\begin{align} T_1 &=& \begin{pmatrix} 0 & 1 & 1 & 1\\ 1/3 & 0 & 0 & 0 \\ 1/3 & 0 & 0 & 0 \\ 1/3 & 0 & 0 & 0 \\ \end{pmatrix} \end{align}$$
Son vecteur propre est : $$\begin{align} \vec{V_1} &=& \begin{pmatrix} 1/2 \\ 1/6 \\ 1/6 \\ 1/6 \\ \end{pmatrix} \end{align} $$
On vérifie l’égalité : $$\begin{align} T_1.\vec{V_1} = \vec{V_1} \end{align} $$
La probabilité d’écouter la version longue est : $$ \frac{P(S2) + P(S3) }{P(S1) + P(S2) + P(S3)} = \frac{2}{3} $$
On retrouve les résultats obtenus précédemment.
Pour la seconde version on obtient un graphe différent : au sortir de S2 on passe par S3 grâce à l’hypnose. De plus, si l’on renouvelle l’expérience le jour suivant, on passe de S1 ou S3 vers S0, mais le passage direct de S2 à S0 n'existe plus.
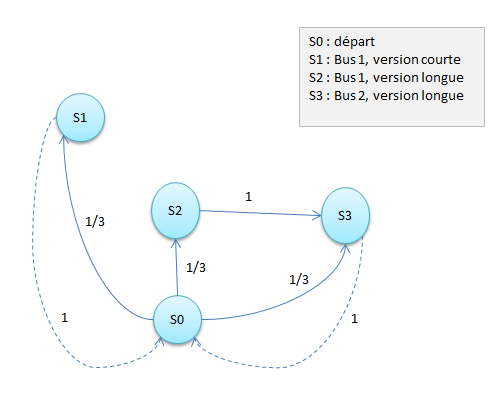
La matrice de transition est : $$\begin{align} T_2 &=& \begin{pmatrix} 0 & 1 & 0 & 1 \\ 1/3 & 0 & 0 & 0 \\ 1/3 & 0 & 0 & 0 \\ 1/3 & 0 & 1 & 0 \\ \end{pmatrix} \end{align} $$
Son vecteur propre est : $$\begin{align} \vec{V_2} &=& \begin{pmatrix} 3/7 \\ 1/7 \\ 1/7 \\ 2/7 \\ \end{pmatrix} \end{align} $$
On vérifie l’égalité : $$\begin{align} T_2.\vec{V_2} = \vec{V_2} \end{align} $$
La probabilité d’écouter la version longue est : $$\begin{align} \frac{P(S2) + P(S3)}{P(S1) + P(S2) + P(S3)} = \frac{3}{4} \end{align} $$
Grâce à la lecture de la matrice de transitions, on peut aussi remarquer que si Fabienne prend n fois le bus, on se posera 4/3*n la question « Version courte ou longue ? ».
Si la notion d’états est possible, la chaîne de Markov permet d’illustrer un processus, et si l’on maîtrise la notion de vecteur propre de fournir les résultats.
