Le pâté d’alouette et la Répression des fraudes

Passons à une utilisation fallacieuse du théorème de Bayes en étudiant une plaisanterie classique chez nos grands-parents. Le pâté d’alouette n’est pas pur à 100%, mais seulement à 50% : un cheval pour une alouette… ! Dans la proportion d’un animal pour un animal (et non pas 1 gramme pour 1 gramme).
Imaginons un producteur de pâté qui utiliserait cette recette aux proportions originales et qu’il soit de mauvaise foi. Toute ressemblance avec un cas connu ne peut qu’être fortuite. Il affirme que son pâté est fait avec une jolie alouette, dont il reçoit 100 grammes de viande et qu’il ne traite que le meilleur, soit 20 grammes. Ajoutons un peu de cheval : sur 700 kilos livrés, il n’en utilise que 140 kilos. Mélangeons bien les 140,020 kg de cette délicieuse mixture. On obtient ce résumé pour les ingrédients :
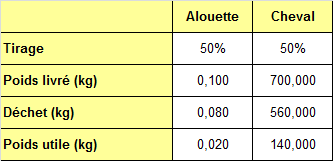
Que ce soit pour l’alouette et le cheval, on ne traite que 20% du meilleur :
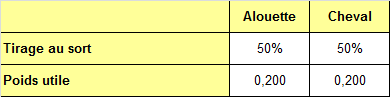
Pour l’instant, rien n’est répréhensible. Mais en malmenant la formule de Bayes, qui se retourne dans sa tombe, il déduit qu’une fibre de viande prise au hasard dans une conserve a autant de chance de venir de l’alouette que du cheval !
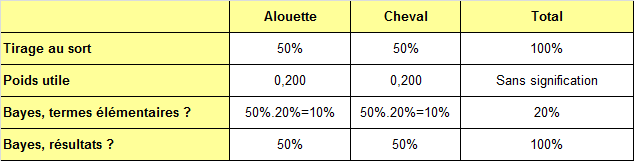
Question
La Répression des Fraudes veille et ne goûte pas à ce genre de calcul ! On peut se demander si impliquer la théorie des probabilités est le meilleur moyen de réfuter le raisonnement fallacieux notre producteur indélicat.Néanmoins, il serait bien de voir pourquoi la formule Bayes « indiquait » un résultat ahurissant ! Voyez-vous comment appliquer correctement le formule de Bayes ? Si vous parvenez à trouver la réponse, faites un graphe ou un tableau, car cela sera utile pour maîtriser les problèmes qui suivent.
Réponse
Simplement en l’utilisant de façon erronée. Avec deux graphes on retrouve l’emploi normal de formule de Bayes :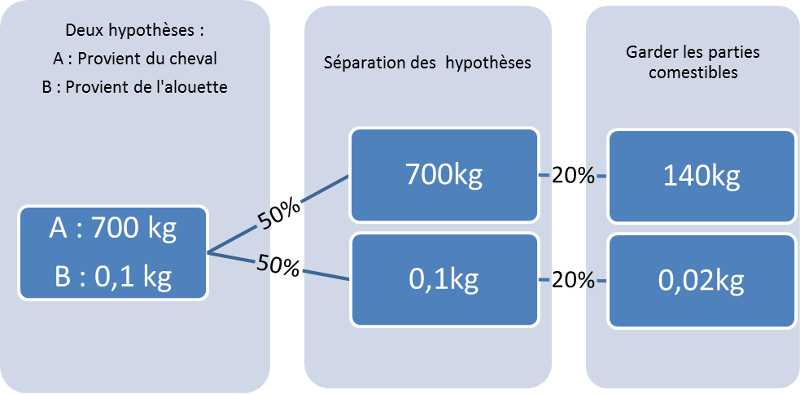
Avec quelques transformations, on aboutit à :
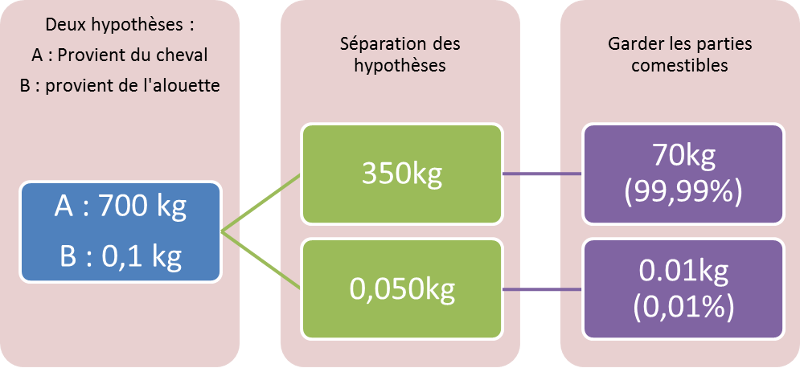
On est bien sûr très loin des 50% de départ affirmés par notre producteur !
Il a calculé :
\[P(Alouette|E) = \frac {0,50}{0,50+0,50}...???\]
En réalité, la formule de Bayes donne :
\[P(Alouette|E) = \frac{0,50.700}{0,50.700+0,50.0,1}=99,99\%\]
Notre producteur voulait nous faire confondre moyenne et moyenne pondérée.
Ici, en manipulant une grandeur physique (un poids bien réel et non pas un pourcentage cuisiné à la va-vite), un consommateur ne peut pas tomber dans le panneau.
