L’Argument de l’Apocalypse

Le paradoxe de Leslie (c’est l’un de ses autres noms (9)) repose lui aussi sur l’utilisation de la formule de Bayes.
Imaginons (il n’y a rien de réel) que quelque part existent des mondes dont leurs issues seraient soumises à deux hypothèses que l’on met en concurrence (10):
- La théorie A : l’humanité du monde considéré disparaîtra en 2150 ;
- La théorie B : l’humanité du monde considéré disparaîtra plus tard.
- Selon la théorie A, un humain sur 10 aura connu l’an 2000. On aura donc 5 milliards de personnes ayant vu l’an 2000 sur un total de 50 milliards à travers les âges.
- Dans le cas B, l’humanité considérée aura alors eu une population plus large. Pour fixer les calculs, disons qu’un humain sur 1000 aura connu l’an 2000. Là aussi 5 milliards de personnes auront vu l’an 2000, mais sur un total de 5 000 milliards de personnes.
- la théorie A a une chance sur 100 d’exister (ou d’être en cours) ;
- quant à la théorie B, on lui donne 99% de chance d’exister.
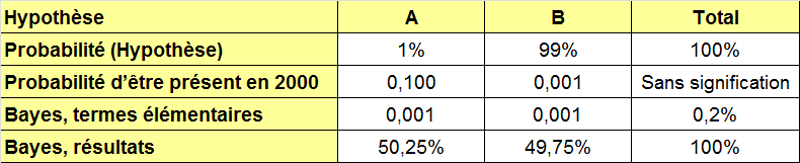
D’où vient ce changement ?
- D’un côté, je peux affirmer que le lien entre entre l’événement E et les hypothèses A (« je suis tombé dans un monde fou !) ») et B (« j’ai peu de raisons de m’en faire ») n’a ici aucune importance et je ne peux pas appliquer la formule de Bayes.
- D’un autre, je peux dire qu’il y a un événement E tout à fait digne d’intérêt et à prendre en compte .
- Ainsi, certains avancent que la formule Bayes ne serait pas applicable ici.
- D’autres ajoutent des considérations supplémentaires, mais cela revient à changer les hypothèses du problème.
- J’aurais mieux fait de ne connaître ni Carter ni l’An 2000, car le calcul serait exact !
Question
En vous inspirant des pages précédentes, pouvez-vous rectifier les calculs ?Réponse
Plus rationnel, le mathématicien français Jean-Paul Delahaye démontre que l’emploi de la formule de Bayes est source de pièges et a proposé une explication dans (11) et (12). On peut aussi se rappeler le Pâté d’alouette (ou voir (13)) et rectifier le tableau vu plus haut.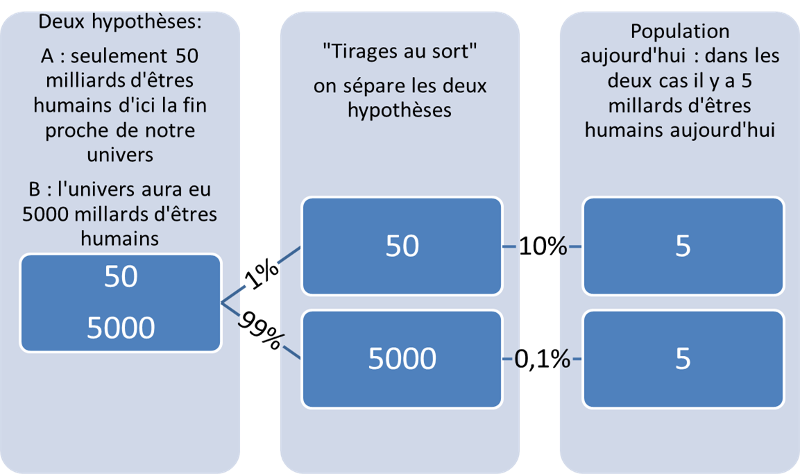
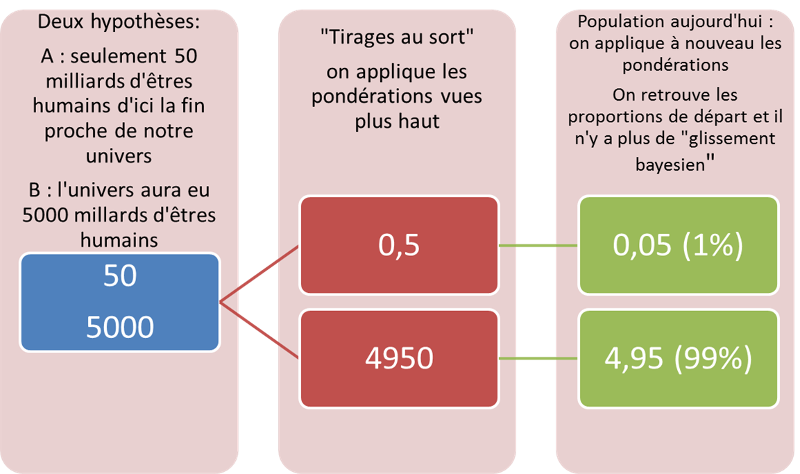
\[P(B|E)=\frac{0,1\%.99%}{0,1\%.99\%+10\%.1\%}...???\] L’exercice n’est pas trop différent de celui du pâté d’alouette, mais les chiffres mis en jeu sont notablement différents. Et une erreur de raisonnement est vite arrivée !
On peut se demander où était le piège ? Maintenant que tout est au grand jour, chacun peut choisir sa méthode de raisonnement :
- Jean-Paul Delahaye parle d’anamorphoses (c’est-à-dire une forme de déformation), d’effet de loupe ou de filtre (on ne regarde que les 5 milliards d’individus présents en l’an 2000).
- La confusion entre moyenne et moyenne pondérée est la cause du raisonnement fallacieux.
- L’événement E n’apporte aucune information (14) et il n’y pas lieu de faire des calculs inutiles (si on l’on passe outre, c’est un droit, mais cela n’autorise pas à faire dire n’importe quoi à Bayes).
Conclusion
Selon une formule célèbre, « Un topologue est une personne qui ne connaît pas la différence entre une tasse de café et un beignet ». Maintenant, on peut dire qu’ « un probabiliste est une personne qui connaît la ressemblance entre l’Apocalypse et un pâté d’alouette ».____________
(9) On peut affirmer que l’usage a validé un anglicisme. « Argument » se traduit ici par « Débat ».
(10) On reprend ici la formulation présentée par Jean-Paul Delahaye, Au pays des paradoxes, Belin, Pour la science, 2008
(11) Jean-Paul Delahaye, Au pays des paradoxes, Belin, Pour la science, 2008
(12) "La Belle au bois dormant, la fin du monde et les extraterrestres" par Jean-Paul Delahaye. © Pour la science -N° 309 juillet 2003. Article ici .
(13) Philippe Gay, Édouard Thomas, Détournement de Bayes, Tangente n°136, Septembre-Octobre 2010
(14) Il existe sans doute plusieurs façons d’expliquer pourquoi E n’apporte aucune information. Si ceci est admis, il n’y a plus besoin de faire de longs calculs. Mais il resterait une énigme : pourquoi Bayes serait incohérent et nous mettrait sur une fausse piste ? Pour un probabiliste, il est tout aussi important de voir que la formule de Bayes n'est pas erronnée.
