Les biscuits d’Alice et de Béatrice

Le « sachant E » (que l'on note "|E") peut aller jusqu’à contredire les premières observations.
Pour illustrer cela, imaginons une charmante histoire qui illustre la formule de Bayes (1). Il s'agit de comparer probabilités et probabilités conditionnelles.
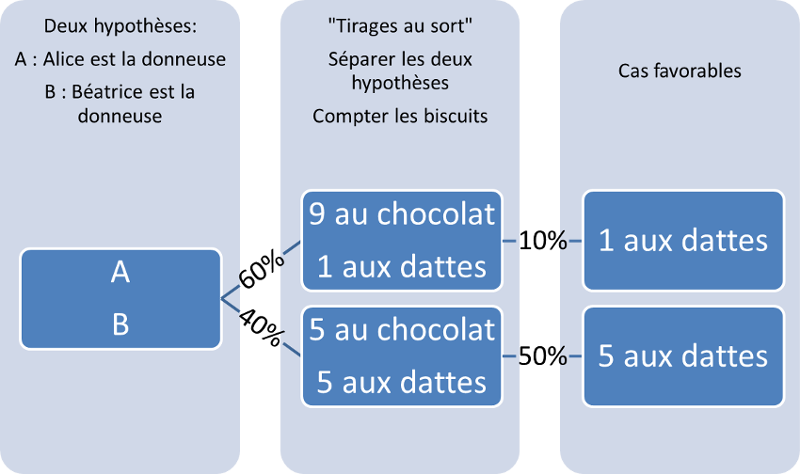
Alice pour son quatre-heures, dispose d’une boîte de dix biscuits :
- neuf au chocolat ;
- et un aux dattes.
- cinq au chocolat ;
- et cinq aux dattes.
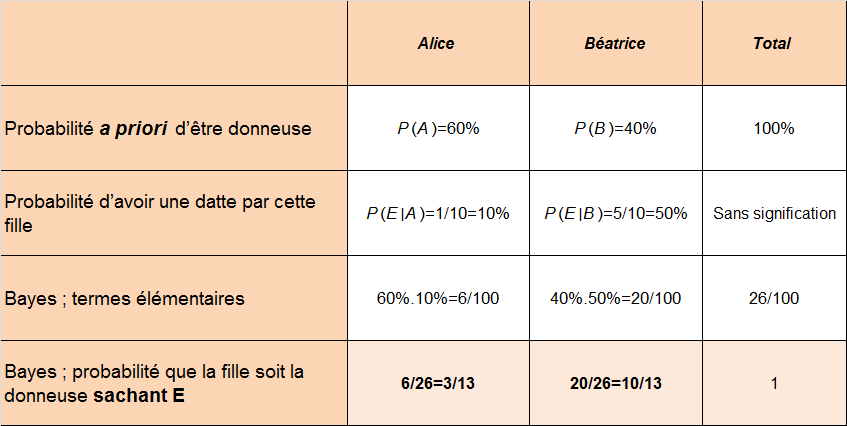
- Alice a 60% de chances d’être la donneuse ;
- et Béatrice 40%. Ces possibilités sont notées A et B.
- \(P(A)=60\%\)
- \(P(B)=40\%\)
Je suppose que chaque biscuit au sein d’une boîte a autant de chance d’être choisi par Marguerite que les neuf autres. Sans faire de calculs, chacun peut dire :
- \(P(A) > P(A|E)\) : mon observation de E, c’est-à-dire le biscuit aux dattes dans la main de Marguerite, me donne quelques doutes sur la générosité supposée d’Alice.
- \(P(B) < P(B|E)\) : le quasi monopole de Béatrice sur les biscuits aux dattes m’incite à reconsidérer mon évaluation de départ en sa faveur.
\[P(A|E)=\frac{P(A).P(E|A)}{P(A).P(E|A)+P(B).P(E|B)}\] De façon similaire :
\[P(B|E)=\frac{P(B).P(E|B)}{P(A).P(E|A)+P(B).P(E|B)}\] On vérifie :
\[P(A|E)+P(B|E)=1\]
Ces calculs permettent d’obtenir un rapport \(P = \frac {\text{Nombre de cas favorables}}{\text{Nombre de cas possibles}}\) plus précis par notre connaissance de l’événement E.
Il est souvent plus commode et plus sûr d’éviter de présenter la réponse sous sa forme littérale comme ci-dessus et de choisir une représentation plus claire [8] :
- sous forme de tableau, qui permet une vérification rapide ;
- ou sous forme de graphes, qui guidera votre raisonnement.
Tableau
Graphes
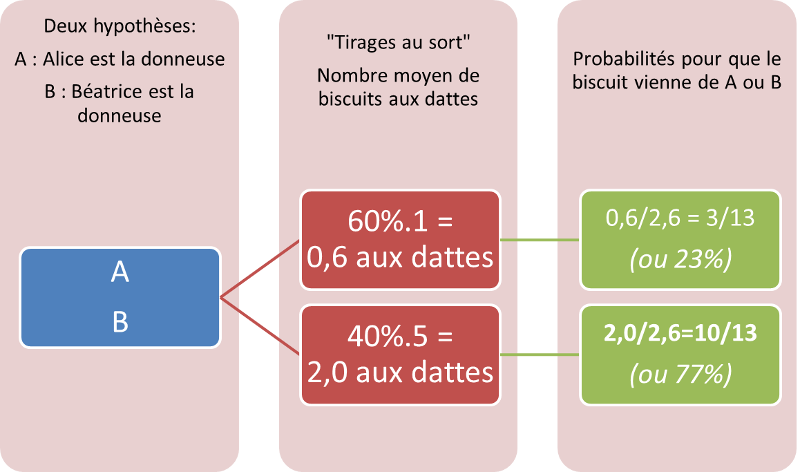
Conclusion
Béatrice avait une probabilité de seulement 40% d'être la donneuse. Mais connaître E m'a fait changer d'avis : Béatrice a maintenant 77% d'être la bonne copine.
Dans cet exemple, le « sachant E » change fortement les probabilités.
____________
(1) Thomas Bayes (1702, 1761), mathématicien britannique et pasteur de l’Église presbytérienne.
