Les 24 heures du Mans

Henry, un célèbre directeur d’une marque automobile, affirme : « Je n’envisage que deux hypothèses. Soit mes voitures engagées aux 24 heures du Mans cassent au bout de 4 heures, soit elles vont au bout et gagnent. »
On note respectivement Hypothèse A et Hypothèse B ces deux issues possibles, et on suppose qu'il n'y en a pas d'autres.
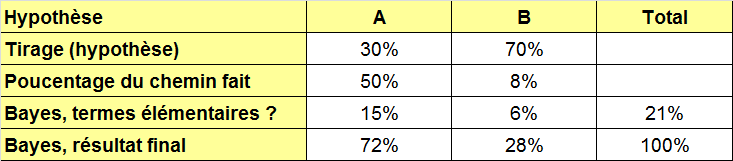
On obtient ce tableau en supposant que la deuxième hypothèse soit plus probable (disons 70%) :

Au bout de deux heures, on fait la moitié du chemin pour l’hypothèse A et bien moins (8,3%) pour l’hypothèse B. L’adversaire direct d’Henry, Enzo, applique à sa façon la formule de Bayes et obtient ce tableau. Il assimile les heures à des événements, donc à des probabilités. D'après Enzo, la fin de la ronde des voitures d’Henry serait proche. Le tableau montre ce que l’on peut appeler un glissement Bayessien qui est choquant, car on chute de 70% à 28% de taux de réussite :
Henry n’y comprend rien ! Pour l’instant, tout se passe bien pour lui. Comment ces deux heures ont pu dégrader la situation ? La formule de Bayes serait-elle erronée ?
Toutefois Stirling, l’un des ingénieurs motoristes d’Henry, voit comment appliquer la formule de Bayes.
Question
Comment Stirling a-t-il remis les chiffres en bon ordre et rassuré son patron ?
Réponse
D'abord, on peut se demander si les calculs d'Enzo prennent en compte le fait que les voitures d'Henry roulent ou non au bout de 2 heures ! Si ce n'est pas le cas, la suite est fausse.Quant à Bayes, même si Enzo trouvait le moyen de justifier l'assimilation heures-probabilités, il faudrait corriger les calculs d'Enzo.
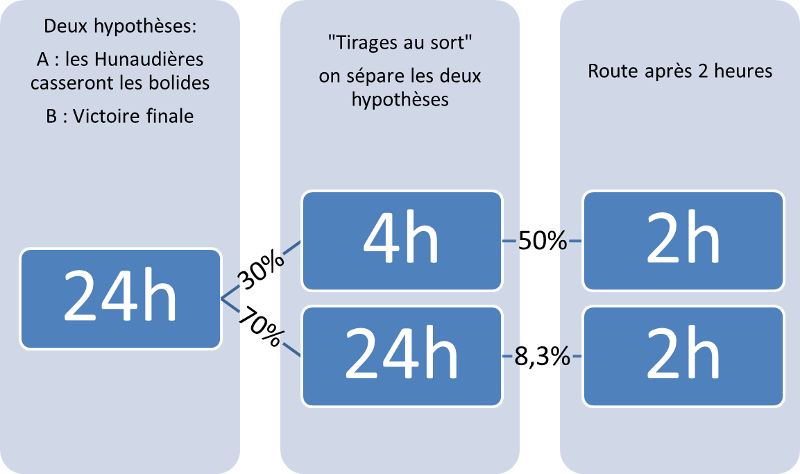
Avec quelques aménagements, on obtient le résultat correct :
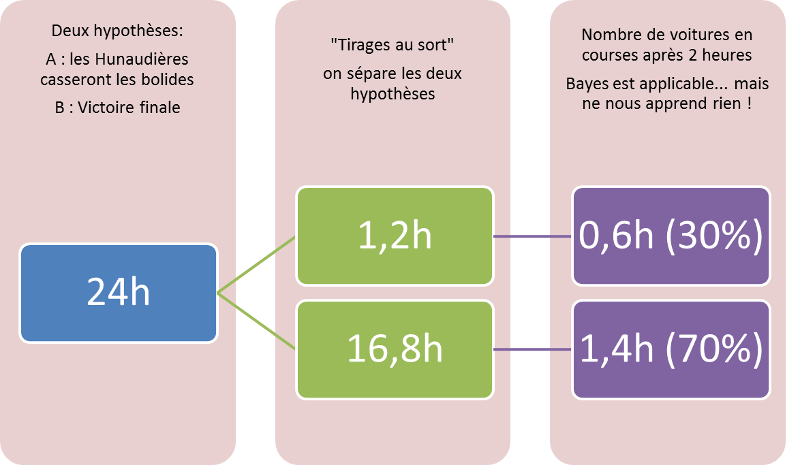
A nouveau, la formule de Bayes « retombe sur ses pieds ». L'observation d'Enzo n'apporte rien, car on retrouve les probabilités de départ : \[P(A) = P(A|E) = 30\% ;\] \[P(B) = P(B|E) = 70\%.\]
En réalité, ce calcul suppose une dégradation de l’état des voitures simple à calculer : autant de pannes (un expert parlerait d’événements) pour chacune des heures qui passent. Des hypothèses et un calcul plus complexes ne changeraient pas la conclusion : le calcul d’Enzo n’est pas défendable. L’important est ici de mettre en avant une forme de raisonnement qui au minimum évite les aberrations.
Si on prenait quelques précautions, on pourrait affirmer que les voitures d'Henry feraient une moyenne de 18 heures de courses (soit 1,2 h + 16,8 h). Pourquoi pas, mais on peut aussi dire que c'est le genre de manipulations de chiffres qu'il est difficile d'interpréter. Cette moyenne est bien sûr sur l'ensemble du parc de voitures, mais on ne sait pas sans plus d'informations si cela se voit sur une seule épreuve ou sur plusieurs. Dans le second cas, c'est impossible à vérifier.
La réalité a déjà dépassé la fiction : aux 24 heures du Mans 1965, toutes les Ford abandonnent en quelques petites heures. L'année suivante, elles battent tous les records.
